Investorsapiens.de – AktienAnalysen und Finanzartikel 2024
Ausführliche Aktienanalysen, Finanzfeed, Erfahrungsberichte und Tests. Finanzielle Bildung, Vermögensaufbau und Altersvorsorge.
Willkommen im Investorsapiens.de News und Aktienanalysen Bereich
Hier findest du eine ausgewogene Mischung aus Finanzwissen, aktuellen Finanzthemen und ausführlichen Aktienanalysen.
Abonniere gerne den Newsletter und folge mir auf meinen Social Media Kanälen, um immer top informiert zu bleiben, exklusiven Content zu erhalten und keine Analyse zu verpassen.
Finanzfeed: Artikel der Woche

Die besten ETFs für die Zukunft (für Anfänger) 2024
Die besten ETFs für die...
Nächster Beitrag
Tag(e)
:
Stunde(n)
:
Minute(n)
:
Sekunde(n)
Folge mir auf meinen Social Media Kanälen
Grundlagen des Vermögensaufbaus und des Investierens
Lerne in 5 Abschnitten: Einstieg, Vermögensaufbau, Strategie und Analyse alles was du über die Börse und den Vermögensaufbau wissen musst. Mein komplettes Wissen aus 16 Jahren Börse kostenlos für dich in einer Anleitung für Anfänger zusammengefasst.
Finanzblog News und Aktienanalysen der vergangenen Wochen
Finanzfeed + Aktienanalysen der vergangen Wochen
Hier findest du eine Übersicht der neuesten Finanzartikel und Aktienanalysen der vergangenen Wochen und Monate. Die Themenwahl erfolgt auf Basis der neuesten Entwicklungen in der Finanzwelt, bedeutender Trends und der allgemeinen wirtschaftlichen Lage. Diese Analysen dienen nicht nur der Zusammenstellung meines eigenen Portfolios auf investorsapiens.de, sondern bieten auch spannende Einblicke in vielversprechende Aktien.
Aktienanalysen
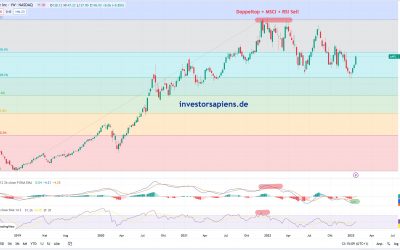
Novo Nordisk Aktie kaufen oder nicht? Analyse 2024
Novo Nordisk Aktie kaufen...
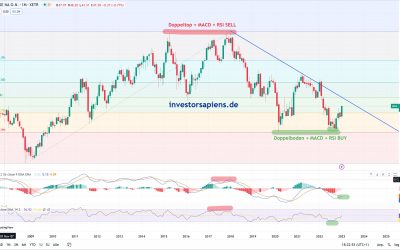
Bayer Aktie am 20-Jahres-Tief. Aktienanalyse 2024
Bayer Aktie am...
Wahl der Aktienanalyse März 2024 (10 Aktien)
Wahl der Aktienanalyse 2024...
Realty Income Dividende Aktienanalyse 2024
Realty Income Dividende...
AMD Aktienanalyse 2024: KI Beschleuniger
AMD Aktie Prognose 2025AMD...
SPLUNK Aktie Prognose KI Megatrend 2023
Splunk Aktie Prognose - KI...
TUI-Aktie Prognose 2025: Aktienanalyse 2023
TUI-Aktie Prognose 2025 und...
PayPal Aktienanalyse 2023 A14R7U
PayPal Aktienanalyse 2023...
Medical Properties Trust 2023: Droht Zahlungsausfall?
Medical Properties Trust...
Allianz Aktienanalyse 2023: Defensiver Dividendenkern
Allianz Aktienanalyse 2023...
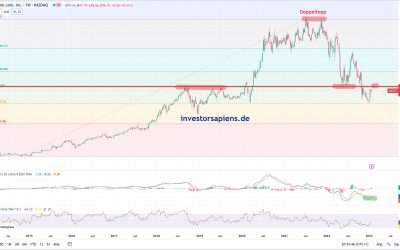
ETSY Aktienanalyse 2023: Hedgefonds ermittelt
ETSY Aktienanalyse 2023...
NVIDIA Aktienanalyse 2023: Die Nummer 1 der KI
NVIDIA Aktienanalyse 2023...
Alphabet Aktienanalyse 2023: Kampf der KI!
Alphabet Aktienanalyse 2023...
Microsoft Aktienanalyse 2023: Vorreiter bei KI!
MICROSOFT Aktienanalyse 2023...
Meta Aktienanalyse 2023: #1 Social Media mit 77% Rabatt?
Meta Aktienanalyse 2023...
APPLE Aktienanalyse 2023: 31% Korrektur beendet?
APPLE Aktienanalyse 2023...
BASF Aktienanalyse 2023: 60% Kurssturz?
BASF Chartanalyse...
Amazon Aktienanalyse 2023: Absturz um 56%?
AMAZON.COM Aktienanalyse...
TESLA Aktienanalyse 2023: Kaufen nach 75% Absturz?
TESLA Aktienanalyse 2023...
3 kostenlose Bestseller deiner Wahl geschenkt!
Hier zeige ich dir völlig kostenlos und unverbindlich, wie du 3 Finanzbücher deiner Wahl geschenkt bekommst.
Finanzartikel, Erfahrungsberichte und Tests
ETF Rentenversicherung Vergleich mit ETF Sparplan
ETF Rentenversicherung...
Budgetplaner – finanziell sicheres Leben mit einem Budgetbuch
Budgetplaner - finanziell...
Comdirect Junior Depot – Geldanlage für Kinder und Enkel Juniordepot 2024
Comdirect Junior Depot:...
Die besten ETFs für die Zukunft (für Anfänger) 2024
Die besten ETFs für die...
Privatier werden – 3 Strategien zur finanziellen Freiheit und Leben ohne Arbeit
Privatier werden - 3...
Trade Republic Einladungscode GVSRT38G
Trade Republic...
Junior Depot Vergleich – Das beste Depot für Kinder 04/2024
Junior Depot Vergleich - Das...
Woolsocks App Erfahrungen: Cashback Finanz-App im Test 2024
Woolsocks App Erfahrungen -...
Quirion Erfahrungen: Robo-Advisor Test 2024 (+100 Euro)
Quirion Erfahrungen - der...
Jahresrückblick 2023: +147 % mit 14 Aktienanalysen
Jahresrückblick 2023 -...
Consorsbank Junior Depot: Schritt für Schritt Anleitung
Consorsbank Junior Depot...
Megatrend Künstliche Intelligenz: KI Aktien 2024
Megatrend KI Aktien: OpenAI Aktie kaufen 2023
Notgroschen: Der ultimative Guide 2023
Finanzieller Notfall Guide:...
Nachhaltig investieren in erneuerbare Energien
Nachhaltig investieren in...
Portfolio Tracking App Getquin
Beste Portfolio Tracking App...
Finanzblog
Finanzielle Bildung und Aktienanalysen 2024
Willkommen bei investorsapiens.de, deinem deutschsprachigen Finanzfeed für finanzielle Bildung, Aktienanalysen, Aktien und ETFs!
Hier findest du eine ausgewogene Mischung aus Finanzwissen (über 16 Jahre Erfahrung als erfolgreicher Investor), ausführlichen Finanzrecherchen und hochwertigen Aktienanalysen (inkl. Zahlen und Fakten, Analystenmeinungen und Chartanalysen). Ich beschäftige mich seit Jahren mit dem Thema KI und habe in den letzten zwei Jahren mehrere Analysen veröffentlicht, die sich rückblickend als Gold wert erwiesen haben.
Die Finanzindustrie und das Investieren können auf den ersten Blick komplex erscheinen. Deshalb habe ich mein Finanzwissen in fünf Abschnitten in einer Schritt-für-Schritt-Anleitung zusammengefasst und die Welt der Finanzen verständlich erklärt. Ich gebe dir hilfreiche Tipps, zeige dir Investitionsmöglichkeiten auf und erkläre dir den Finanzmarkt, damit du deine eigenen Entscheidungen treffen, deine eigenen Investitionen tätigen und mit deiner eigenen Geldanlage beginnen kannst.
Finanzbildung ist der Schlüssel zum Erfolg. Deshalb biete ich dir kostenlosen Zugang zu meinen zahlreichen Artikeln und Aktienanalysen und gebe dir Tipps, wie du die besten Finanzbücher kostenlos bekommst. Damit möchte ich dich beim Investieren und beim Vermögensaufbau unterstützen und dir helfen, finanziell frei zu werden. Beginne noch heute deinen Weg zur finanziellen Freiheit und finde Anlagetipps in einem der besten Finanzblogs Deutschlands.
Ich bin davon überzeugt, dass finanzielle Freiheit und eine sichere Altersvorsorge für jeden erreichbar sind. Egal ob du dich auf deinen Ruhestand vorbereiten, deine Familie finanziell absichern, ein Juniordepot für deine Kinder suchst oder ein Vermögen aufbauen möchtest, ich habe alle Informationen, die du für einen einfachen Einstieg in das Thema Finanzen brauchst.
Finanzblog Beiträge
Allgemeine Beiträge
Hier findest du sonstige allgemeine Finanzthemen.
Generationenvertrag – Probleme und Lösungen
Generationenvertrag -...
Als Frau schnell Geld verdienen: 17 Nebenjobs 2024
17 Nebenjobs mit den du als...
One Day or Day One – Jetzt ist die beste Zeit zum Investieren
One Day or Day One - Jetzt...
Wie viel Geld braucht man zum Leben?
Wie viel Geld braucht man...
Audible 3 Monate Gratis (3 Finanzbücher für 0,00 Euro)
Audible 3 Monate Gratis (10...
Jahresrückblick 2023: +147 % mit 14 Aktienanalysen
Jahresrückblick 2023 -...
Amazon Kreditkarte Nachfolger
Amazon Visa Kreditkarte gesperrt. Hier findest du eine Alternative
Aus der Geldnot in die finanziellen Freiheit
Kredit in 1 Stunde auf Konto...
StockGPT im Praxistest: KI-Finanzassistent
Stock GPT im Praxistest:...
Persönlichkeitsentwicklung
Insights einer Führungskraft. Mit Persönlichkeitsentwicklung Büchern zum Erfolg.
Wie viel Geld gibt es auf der Welt?
Wie viel Geld gibt es auf...
Sparen und Anlegen trotz 8,7 % Inflation in Deutschland 2023
Sparen und Anlegen trotz 8,7...